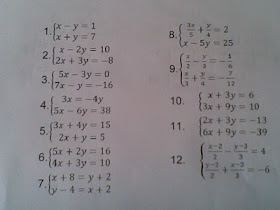domingo, 31 de octubre de 2010
sábado, 30 de octubre de 2010
MÉTODO DE DETERMINANTES
MÉTODO DE REDUCCIÓN
MÉTODO DE IGUALACIÓN
MÉTODO DE SUSTITUCIÓN
MÉTODO GRAFICO
jueves, 28 de octubre de 2010
Módulo 5 - Actividad Final
NOMBRE DEL PROFESOR ING. Víctor Gabriel Oliva Huerta
NIVEL ACADÉMICO Y SUBSISTEMA O DISCIPLINA COLEGIO DE CIENCIAS Y HUMANIDADES
PLANTEL AZCAPOTZALCO
ASIGNATURA MATEMÁTICAS
SEGUNDO SEMESTRE
UNIDAD TEMÁTICA Y CONTENIDOS UNIDAD 1
Situaciones que involucran cambio y que dan origen a funciones cuadráticas.
Comparación de la función cuadrática con la función lineal.
Intersecciones de la gráfica de una función cuadrática con el eje x.
Estudio gráfico y analítico de la función: y=ax^2+bx+c, casos particulares:
y=〖ax〗^2,
y=〖ax〗^2+c,
y=a〖(x-h)〗^2,
y=a(x-h)^2+k.
Concavidad, máximo o mínimo.
Problemas de máximos y mínimos. Resolución algebraica.
POBLACIÓN ESTUDIANTES DE MATEMÁTICAS 2.
SEGUNDO SEMESTRE.
Grupos aproximados de 25 alumnos.
DURACIÓN 5 horas clase (dos sesiones de 2 horas y una de 1 hora) y 5 horas extra clase.
PROPÓSITOS QUE EL ALUMNO :
Analizar los datos que originan una función cuadrática.
Determinar las características de una función cuadrática realizando su grafica.
Determinar las diferencias que hay entre una función lineal y una cuadrática.
Analizar a partir de la grafica las intersecciones con el eje de las abscisas.
Analizar el comportamiento de una función cuadrática tabulando, algebraicamente y gráficamente.
Determinar el vértice de una función cuadrática.
Determinar qué elementos cambian la posición de las funciones cuadráticas.
HABILIDADES DIGITALES Uso de INTERNET
Nivel 1 (básico):
Búsqueda de información, como complemento de una investigación de medios impresos.
Búsqueda y selección de videos sobre información específica.
Justificación: El alumno despertara la habilidad de buscar información en internet verificando su veracidad al compararla con medios impresos.
Como medio de comunicación
Nivel 1 (básico):
Uso de correo electrónico,
Uso de foros, para opinar sobre temas específicos, investigados previamente.
Uso de una red social (FACEBOOK).
Justificación: Es importante que los alumnos cuenten con una cuenta de correo electrónico y pertenezcan a una red social. La utilización de un foro como parte de un debate o intercambio de opiniones es importante porque hace que el alumno lea de forma inmediata lo que piensan los demás participantes.
Como medio de creación
Nivel 1 (básico):
Uso de blog para producir contenidos,
Inclusión de ligas a videos.
Justificación: En el blog los alumnos podrán exponer sus trabajos terminados, subir algunos videos relacionados con el tema e incluso fotos.
Nivel 2 (avanzado):
Para creación y publicación de videos.
Justificación: Los alumnos también podrán realizar videos, en los cuales podrán exponer los temas que realizaron.
Uso seguro de las TIC
Nivel 1 (básico):
Descarga de archivos y programas,
Uso seguro del correo electrónico,
Uso seguro de blogs,
Configuración segura de redes sociales,
Evitar envió de archivos o fotos importantes en foros, chats y redes sociales.
Justificación: Bueno como ya es un tema que se habla recurrentemente hay que tener cuidado con la información que se proporciona en las redes sociales y no solo con la información si no lo que se llega a publicar sin una autorización.
Como también saber qué tipo de información podemos abrir, ya que luego se abren correos electrónicos que contienen algún tipo de virus de personas desconocidas, así como también de nuestros compañeros que llegan a tener virus sin que ellos lo sepan. Es por ello que debemos contar con un antivirus eficaz. En cuanto a virus, pero también se tiene que tener cuidado en el perfil que proporcionamos en el correo, es por ello que se tiene que explicar y decir a los alumnos que tengan cuidado incluso en a quien proporcionan o dan los permisos necesarios para tener acceso a su perfil.
Presentación de información y procesamiento de datos
Nivel 1 (básico):
Manejo básico para procesar datos,
Manejo básico de software especializado.
Hoja de cálculo para presentar tablas y gráficos.
Justificación: Es claro que el alumno tiene que presentar las actividades con una buena presentación, es por ello que deberán conocer y manejar en forma básica tanto un procesador de datos, el software y la hoja de cálculo.
Manejo de medios
Nivel 1 (básico):
Uso básico de celular y cámaras de fotos y video.
Nivel 2 (avanzado):
Edición de imágenes, audio y video.
Producciones de imágenes audio o video en software libres.
Justificación: No olvidemos que en algunos casos una imagen habla más que mil palabras, es por ello que el alumno deberá de ser capaz de manejar algún aparto, ya sea celular, cámara fotográfica o de video, para captar algunas imágenes o momentos que puedan explicar de forma visual el problema a desarrollar. Es por ello que también se les proporcionara las herramientas necesarias, para editar fotos o videos.
Recursos tecnológicos y Software
Nivel 2 (avanzado):
Instalación y manejo básico de software especializado.
Justificación: En la actualidad se cuentan con software que facilitan la comprensión grafica de algunos problemas, es por ello que se proporcionara una forma fácil de instalar un software libre para poder graficar estos problemas y poder manejar en una forma sencilla y básica.
Organización y administración de la información
Nivel 1 (básico):
Como nombrar archivos de forma específica,
Impresión de archivos,
Descarga e instalación de programas,
Guardado de información en CD o USB.
Justificación: Algunos de estos casos ya sean abordado con anterioridad, pero para facilitar la búsqueda de archivos realizados con anterioridad se tienen que nombrar de alguna forma específica, ya sea para poder imprimirlos o trasladarlos en una memoria y detectarlos rápido.
Nivel 2 (avanzado):
Compresión y descompresión de archivos,
Descarga y subida de archivos,
Eliminación de archivos innecesarios.
Justificación: En algunas ocasiones con la finalidad de que un archivo no ocupe mucho espacio se tienen que comprimir, para poder enviarlos, es por ello que el alumno debe tener la habilidad para poder realizar estos pasos. Bueno y definitivamente subir o descargar archivos, que pienso yo en un correo electrónico es algo básico.
Uso de periféricos
Nivel 1 (básico):
Manejo de ratón y teclado,
Manejo de impresora, cámaras, celular.
Justificación: Es claro que el manejo de ratón y teclado debe de ser fundamental, como también impresoras, cámaras y celulares. Sin embargo creo que se tiene que preguntar o enseñar a algunos alumnos que nunca han tenido contacto con una computadora y mucho menos impresora, ya que un celular y cámara está al alcance de todos.
MATERIALES Material de computo:
Computadora
Acceso a internet
Sistema operativo WINDOWS
Navegador Explorer 7, MOZILLA FIREFOX o GOOGLE CHROME
Memoria de almacenamiento USB
Hoja de calculo
Software GEOGEBRA
Correo electrónico
Procesador de textos.
Documentos PDF, con gráficos y tipografía matemática
Pizarrón
Sala Telmex
Proyector
Plumones.
DESCRIPCIÓN DE LAS ACTIVIDADES
ACTIVIDAD 1
Investigar en Internet y cotejar con algunos libros conceptos como:
Función cuadrática
Grafica de una función cuadrática
Componentes de la grafica de una función cuadrática.
ACTIVIDAD 2
Problemas que dan lugar a una función cuadrática:
Desde un puente peatonal, con altura de 5.50 m, se deja caer verticalmente una pelota. ¿Qué tiempo tardara la pelota en llegar al piso?
Se recurre a una fórmula que relaciona, la distancia, el tiempo y en este caso la gravedad que también es un factor muy importante: d = ½ g t² si sabemos que g = 9.81 m/seg² y tiempo t desconocido.
A completa lo que falta para llegar a una función cuadrática.
________= ½__________ t² si t = x
Transponiendo términos la ecuación queda:
_______x²-_______=0
ACTIVIDAD 3
GRAFICA DE UNA FUNCION CUADRATICA
En GEOGEBRA introduce los datos en la zona de entrada y trazar la grafica de y = x² , y responda las siguientes preguntas:
En este caso si sabemos que la ecuación de una función cuadrática está dada por y=ax²+bx+c. ¿Cuál es el valor de a? ________
El vértice se encuentra en el punto (_____,_____)
La concavidad es ________________
Las ramas abren ________________
El eje de simetría es X = __________
Tiene un valor máximo ó mínimo _______________
Ahora construya la grafica de y = - x² , y responda:
¿Cuál es el valor de a? ___________
El vértice se encuentra en el punto (_____,_____)
La concavidad es ________________
Las ramas abren ________________
El eje de simetría es X = __________
Tiene un valor máximo ó mínimo _______________
Realiza las observaciones que tengas con respecto a las dos graficas. ________________________________________________________________________________________________________________________________________________
ACTIVIDAD 4
FUNCIÓN CUADRÁTICA Y FUNCIÓN LINEAL
En GEOGEBRA realiza los siguientes gráficos en un solo sistema de coordenadas cartesianas:
1) y = x² y y = x (en entrada introduce primero y = x² el cuadrado lo puedes poner con la barra siguiente de entrada, y después y = x) con ayuda de la hoja de cálculo realiza las tablas y realiza los gráficos por separado para obtener el comportamiento de cada tabla.
2) y = x² +1 y y = x + 1 realiza lo mismo que en el inciso anterior.
Ahora realiza las observaciones en cuanto al comportamiento de cada grafico y la diferencia que existe en cada una de las tablas que obtuviste.
Observaciones tabla 1 y = x² y y = x
________________________________________________________________________________________________________________________________________________
Observaciones tabla 2 y = x² + 1 y y = x + 1
________________________________________________________________________________________________________________________________________________
ACTIVIDAD 5
RAICES DE LA ECUACIÓN CUADRÁTICA ASOCIADA A LA FUNCIÓN CUADRÁTICA
La grafica de una función cuadrática permite encontrar de forma visual la solución de la ecuación cuadrática.
Con ayuda de la hoja de cálculo obtén la tabla de valores y la grafica de las siguientes funciones cuadráticas:
f(x) = x² + 2x -8
g(x) = x² - 3x -10
Observa que cada grafica intercepta al eje x en dos puntos Indica el valor de cada punto:
x_1= __________ y x_2=__________
x_1= __________ y x_2=__________
Esos valores son las raíces o soluciones de cada una de las funciones cuadráticas anteriores.
Con ayuda de GEOGEBRA determina las raíces de las siguientes funciones cuadráticas y señale las raíces en el grafico.
f(x) = x² + 3x -10 x_1= ______ y x_2=_______
g(x) = x² + 2x +1 x_1= ______ y x_2= ______
h(x) = x² - x – 30 x_1= ______ y x_2= ______
k(x) = x² + 2x + 3 x_1= ______ y x_2= ______
ACTIVIDAD 6
ANALISIS DE COMPORTAMIENTO DE PARÁMETROS DE LA FUNCIÓN CUADRÁTICA
En un mismo sistema de coordenadas cartesianas realiza la grafica de las siguientes funciones y anota tus observaciones comparando las con x².
y = x² , y =5 x² y y = ¼ x²
Observaciones: ________________________________________________________________________________________________________________________________________________
Ahora realiza lo mismo pero con y = x²+5, y = x²-5 y compara con la grafica de y = x².
Observaciones: ________________________________________________________________________________________________________________________________________________
Realice los mismo pero ahora con y = (x+3)² y y = (x-3)² comparando las una vez más con y = x².
Observaciones: ________________________________________________________________________________________________________________________________________________
ACTIVIDAD 7
VERTICE DE UNA PARABOLA
El vértice de una parábola se representa por V (h, k), y se puede obtener algebraicamente y gráficamente.
Algebraicamente
Sabemos que las funciones cuadráticas se escriben de la forma general y=ax²+bx+c y se puede obtener fácilmente por el método de completar el trinomio cuadrado perfecto para poder expresarlo de la forma estándar y=a(x-h)²+k.
Gráficamente
Con ayuda de GEOGEBRA se puede graficar una función cuadrática y señalar el vértice.
Determina el vértice de la función f(x) = x² - 4x + 1 mediante el método de completar cuadrados y después verifica tu resultado con ayuda de GEOGEBRA señalando el lugar del vértice.
Si sabemos que h= (- b/2a) y que k= c - (b²/4a) se pueden aplicar estas formulas para obtener el vértice.
Determina el vértice de y = x² -2x + 3, si sabemos que a=_____, b=______ y c=______. Entonces aplicamos las fórmulas:
V (- b/2a , c - (b²/4a)
V (- _____/2_______ , _______ - (_____²/4_______))
V(-______, 3-______)
V(______,2)
Determina el vértice de las parábolas por uno de los dos métodos y comprueba tu resultado en GEOGEBRA.
f(x) = x² + 6x + 7
g(x) = x² - 6x + 13
h(x) = x² + 4 x + 1
ACTIVIDAD 8
Determina las características de la función cuadrática h(x) = - x²+ 2x - 4 si su vértice es V (1,-3) con ayuda de GEOGEBRA.
Coeficiente del término cuadrático_______________
Hacia donde abren las ramas_____________________
La concavidad es_______________________________
Se tienen un máximo o un mínimo_________________
El valor del máximo o mínimo es__________________
La ecuación de eje de simetría es x=h, entonces el eje de simetría es x=__________
El valor que corresponde al máximo o mínimo no los proporciona el valor de k.
Esto es f (h) = k por lo tanto vale _________.
ACTIVIDAD 9
Realiza un informe completo de gráficos y actividades y después envía por correo electrónico.
ACTIVIDADES A DESARROLLAR
Investigar diferentes conceptos de función
La creación de un libro ayudara al alumno a comprender un poco más el tema de funciones cuadráticas y podrá desarrollar un conocimiento más de cómo realizar un libro digital en la red.
Libro
Con la información encontrada en la investigación de conceptos de función, tanto impresa como digital. Los alumnos desarrollaran un libro digital.
Descripción de la actividad
Los alumnos desarrollaran un libro digital con los conceptos investigados (claro deberán agregar bibliografía de la fuente en donde encontraron la información en formato APA). Se les proporcionara un a liga en donde podrán ver como se hace un libro digital. Si llegan a tener alguna duda podrán publicar el muro de FACEBOOK algún comentario o duda.
Documentos extra
http://www.youtube.com/watch?v=7Rw20MLyOwk&feature=player_embedded
Situaciones que dan origen a funciones cuadráticas.
Los alumnos participaran en un foro para poder darse cuenta de las opiniones que tienen sus demás compañeros y poder interactuar con ellos vía un foro de debate para poder complementar su aprendizaje.
Foro
El alumno participara en el foro para analizar ejemplos que involucren funciones cuadradas.
Descripción de la actividad
Se propondrán algunos ejemplos que involucren diferentes tipos de funciones, en los cuales los alumnos tendrán que decir si involucran o no una función cuadrática. Si lo es proponer una forma de resolverlo. Al menos tendrán que tener una participación en cada propuesta.
Video: “Aplicación de la función cuadrática” http://www.youtube.com/watch?v=TF2_IjxOtyY consultado el 13 de agosto del 2010.
Paquete de ejercicios que involucran funciones cuadráticas.
Comparación de una función cuadrática con una función lineal.
Los alumnos desarrollaran una tarea en base a un software especializado para desarrollar graficas y poder hacer sus propias conclusiones en cuanto a la actividad desarrollada.
Tarea
El alumno analizara la grafica de una función cuadrática y la comparara con la grafica de una función lineal.
Descripción de la actividad
El alumno con ayuda de GEOGEBRA realizara las gráficas de una función cuadrática y una función lineal. Analizara las diferencias y realizara observaciones de los gráficos y las tablas que llevan al grafico.
Documentos extra
Serie de ejercicios clase
http://docentes.educacion.navarra.es/msadaall/geogebra/videos/index.htm
Intersecciones de la gráfica de una función cuadrática con el eje x.
En esta actividad se desea involucrar al alumno con las formas en que puede aparecer una función cuadrática y realizara sus conclusiones en cuanto que factores realizan cambios en cada grafica.
Tarea
Analizar las intersecciones de una función cuadrática con el eje de las abscisas.
Descripción de la actividad
El alumno con ayuda de GEOGEBRA graficara diferentes ejemplos de funciones cuadráticas. Interpretara el significado de esas intersecciones. Realizara un informe, en el cual exprese sus resultados después de graficar en GEOGEBRA.
Documentos extra
Serie ejercicios clase.
http://www.youtube.com/watch?v=In3qLE1E_II
Estudio gráfico y analítico de la función y=ax^2+bx+c, casos particulares:
y=ax^2,
y=ax^2+c,
y=a(x-h)^2,
y=a(x-h)^2+k.
El alumno desarrollara previamente ejercicios para identificar los valores que generan un cambio y los elementos que componen una función cuadrática. Con ello analizaran y podrán hacer sus conclusiones y comentarios.
Tarea
El alumno analizara las diferentes formas que se puede presentar una función cuadrática.
Descripción de la actividad
Con ayuda de GEOGEBRA el alumno graficara las funciones cuadrática que se presenten en la actividad y realizaran sus observaciones del comportamiento de cada una.
Después de la clase presencial el alumno será capaz de resolver funciones cuadráticas realizando despejes, factorizaciones, completando el trinomio cuadrado perfecto o formula general.
Por lo tanto también presentara un informe con sus procedimientos y resultados.
Concavidad, máximo o mínimo.
Con los análisis realizados en la actividad anterior los alumnos comprenderán y analizaran los componentes de una parábola (grafica de una función cuadrática) y podrán determinar sin su grafica cada uno de estos componentes.
Tarea
El alumno analizara cada uno de los elementos de una función cuadrática.
Descripción de la actividad
El alumno investigara en un libro los procedimientos para encontrar la concavidad, el vértice, el eje de simetría y el máximo o mínimo de una función cuadrática.
Con ayuda de GEOGEBRA localizara cada una de estas características de diferentes funciones cuadráticas y realizara sus observaciones.
Realizara un informe de procedimientos para calcular tales elementos.
Evaluación
Se realizara una evaluación esperando que el alumno plasme los conocimientos adquirido mediante un cuestionario que evaluara dichos conocimientos desarrollados en las actividades realizadas anteriormente.
Cuestionario
Analizar los conocimientos adquiridos en la unidad.
Descripción de la actividad
El alumno entrara a la plataforma para realizar el cuestionario llamado “Función Cuadrática”.
Instrucciones:
Hacer clic en el cuestionario “función Cuadrática”.
Cuando aparezca en la pantalla hacer clic en el botón “pre visualizar el cuestionario ahora”.
Cuando se despliegue el cuestionario, responder cuidadosamente cada una de las preguntas, al finalizar hacer clic en el botón “Enviar todo y terminar”.
Este cuestionario es individual.
BIBLIOGRAFÍA DE CONSULTA PARA EL PROFESOR Raymond A. Barnett (1984). ALGEBRA (Primera edición en español). (Capitulo 11.3 Gráfica de funciones lineales y cuadráticas página 338-347). México: McGraw-Hill.
La Función cuadrática. Parábolas. (Ministerio de Educación. Año 2001). Pagina web Recursos Tic Educación (Descartes 2D):
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Funcion_cuadratica_parabola/index.htm
Ejemplos diversos de webs interactivas de Matemáticas. Diseñadas con GeoGebra por Manuel Sada Allo. Manuel Sada Allo (2005-10)
http://docentes.educacion.navarra.es/msadaall/geogebra/index.htm
NIVEL ACADÉMICO Y SUBSISTEMA O DISCIPLINA COLEGIO DE CIENCIAS Y HUMANIDADES
PLANTEL AZCAPOTZALCO
ASIGNATURA MATEMÁTICAS
SEGUNDO SEMESTRE
UNIDAD TEMÁTICA Y CONTENIDOS UNIDAD 1
Situaciones que involucran cambio y que dan origen a funciones cuadráticas.
Comparación de la función cuadrática con la función lineal.
Intersecciones de la gráfica de una función cuadrática con el eje x.
Estudio gráfico y analítico de la función: y=ax^2+bx+c, casos particulares:
y=〖ax〗^2,
y=〖ax〗^2+c,
y=a〖(x-h)〗^2,
y=a(x-h)^2+k.
Concavidad, máximo o mínimo.
Problemas de máximos y mínimos. Resolución algebraica.
POBLACIÓN ESTUDIANTES DE MATEMÁTICAS 2.
SEGUNDO SEMESTRE.
Grupos aproximados de 25 alumnos.
DURACIÓN 5 horas clase (dos sesiones de 2 horas y una de 1 hora) y 5 horas extra clase.
PROPÓSITOS QUE EL ALUMNO :
Analizar los datos que originan una función cuadrática.
Determinar las características de una función cuadrática realizando su grafica.
Determinar las diferencias que hay entre una función lineal y una cuadrática.
Analizar a partir de la grafica las intersecciones con el eje de las abscisas.
Analizar el comportamiento de una función cuadrática tabulando, algebraicamente y gráficamente.
Determinar el vértice de una función cuadrática.
Determinar qué elementos cambian la posición de las funciones cuadráticas.
HABILIDADES DIGITALES Uso de INTERNET
Nivel 1 (básico):
Búsqueda de información, como complemento de una investigación de medios impresos.
Búsqueda y selección de videos sobre información específica.
Justificación: El alumno despertara la habilidad de buscar información en internet verificando su veracidad al compararla con medios impresos.
Como medio de comunicación
Nivel 1 (básico):
Uso de correo electrónico,
Uso de foros, para opinar sobre temas específicos, investigados previamente.
Uso de una red social (FACEBOOK).
Justificación: Es importante que los alumnos cuenten con una cuenta de correo electrónico y pertenezcan a una red social. La utilización de un foro como parte de un debate o intercambio de opiniones es importante porque hace que el alumno lea de forma inmediata lo que piensan los demás participantes.
Como medio de creación
Nivel 1 (básico):
Uso de blog para producir contenidos,
Inclusión de ligas a videos.
Justificación: En el blog los alumnos podrán exponer sus trabajos terminados, subir algunos videos relacionados con el tema e incluso fotos.
Nivel 2 (avanzado):
Para creación y publicación de videos.
Justificación: Los alumnos también podrán realizar videos, en los cuales podrán exponer los temas que realizaron.
Uso seguro de las TIC
Nivel 1 (básico):
Descarga de archivos y programas,
Uso seguro del correo electrónico,
Uso seguro de blogs,
Configuración segura de redes sociales,
Evitar envió de archivos o fotos importantes en foros, chats y redes sociales.
Justificación: Bueno como ya es un tema que se habla recurrentemente hay que tener cuidado con la información que se proporciona en las redes sociales y no solo con la información si no lo que se llega a publicar sin una autorización.
Como también saber qué tipo de información podemos abrir, ya que luego se abren correos electrónicos que contienen algún tipo de virus de personas desconocidas, así como también de nuestros compañeros que llegan a tener virus sin que ellos lo sepan. Es por ello que debemos contar con un antivirus eficaz. En cuanto a virus, pero también se tiene que tener cuidado en el perfil que proporcionamos en el correo, es por ello que se tiene que explicar y decir a los alumnos que tengan cuidado incluso en a quien proporcionan o dan los permisos necesarios para tener acceso a su perfil.
Presentación de información y procesamiento de datos
Nivel 1 (básico):
Manejo básico para procesar datos,
Manejo básico de software especializado.
Hoja de cálculo para presentar tablas y gráficos.
Justificación: Es claro que el alumno tiene que presentar las actividades con una buena presentación, es por ello que deberán conocer y manejar en forma básica tanto un procesador de datos, el software y la hoja de cálculo.
Manejo de medios
Nivel 1 (básico):
Uso básico de celular y cámaras de fotos y video.
Nivel 2 (avanzado):
Edición de imágenes, audio y video.
Producciones de imágenes audio o video en software libres.
Justificación: No olvidemos que en algunos casos una imagen habla más que mil palabras, es por ello que el alumno deberá de ser capaz de manejar algún aparto, ya sea celular, cámara fotográfica o de video, para captar algunas imágenes o momentos que puedan explicar de forma visual el problema a desarrollar. Es por ello que también se les proporcionara las herramientas necesarias, para editar fotos o videos.
Recursos tecnológicos y Software
Nivel 2 (avanzado):
Instalación y manejo básico de software especializado.
Justificación: En la actualidad se cuentan con software que facilitan la comprensión grafica de algunos problemas, es por ello que se proporcionara una forma fácil de instalar un software libre para poder graficar estos problemas y poder manejar en una forma sencilla y básica.
Organización y administración de la información
Nivel 1 (básico):
Como nombrar archivos de forma específica,
Impresión de archivos,
Descarga e instalación de programas,
Guardado de información en CD o USB.
Justificación: Algunos de estos casos ya sean abordado con anterioridad, pero para facilitar la búsqueda de archivos realizados con anterioridad se tienen que nombrar de alguna forma específica, ya sea para poder imprimirlos o trasladarlos en una memoria y detectarlos rápido.
Nivel 2 (avanzado):
Compresión y descompresión de archivos,
Descarga y subida de archivos,
Eliminación de archivos innecesarios.
Justificación: En algunas ocasiones con la finalidad de que un archivo no ocupe mucho espacio se tienen que comprimir, para poder enviarlos, es por ello que el alumno debe tener la habilidad para poder realizar estos pasos. Bueno y definitivamente subir o descargar archivos, que pienso yo en un correo electrónico es algo básico.
Uso de periféricos
Nivel 1 (básico):
Manejo de ratón y teclado,
Manejo de impresora, cámaras, celular.
Justificación: Es claro que el manejo de ratón y teclado debe de ser fundamental, como también impresoras, cámaras y celulares. Sin embargo creo que se tiene que preguntar o enseñar a algunos alumnos que nunca han tenido contacto con una computadora y mucho menos impresora, ya que un celular y cámara está al alcance de todos.
MATERIALES Material de computo:
Computadora
Acceso a internet
Sistema operativo WINDOWS
Navegador Explorer 7, MOZILLA FIREFOX o GOOGLE CHROME
Memoria de almacenamiento USB
Hoja de calculo
Software GEOGEBRA
Correo electrónico
Procesador de textos.
Documentos PDF, con gráficos y tipografía matemática
Pizarrón
Sala Telmex
Proyector
Plumones.
DESCRIPCIÓN DE LAS ACTIVIDADES
ACTIVIDAD 1
Investigar en Internet y cotejar con algunos libros conceptos como:
Función cuadrática
Grafica de una función cuadrática
Componentes de la grafica de una función cuadrática.
ACTIVIDAD 2
Problemas que dan lugar a una función cuadrática:
Desde un puente peatonal, con altura de 5.50 m, se deja caer verticalmente una pelota. ¿Qué tiempo tardara la pelota en llegar al piso?
Se recurre a una fórmula que relaciona, la distancia, el tiempo y en este caso la gravedad que también es un factor muy importante: d = ½ g t² si sabemos que g = 9.81 m/seg² y tiempo t desconocido.
A completa lo que falta para llegar a una función cuadrática.
________= ½__________ t² si t = x
Transponiendo términos la ecuación queda:
_______x²-_______=0
ACTIVIDAD 3
GRAFICA DE UNA FUNCION CUADRATICA
En GEOGEBRA introduce los datos en la zona de entrada y trazar la grafica de y = x² , y responda las siguientes preguntas:
En este caso si sabemos que la ecuación de una función cuadrática está dada por y=ax²+bx+c. ¿Cuál es el valor de a? ________
El vértice se encuentra en el punto (_____,_____)
La concavidad es ________________
Las ramas abren ________________
El eje de simetría es X = __________
Tiene un valor máximo ó mínimo _______________
Ahora construya la grafica de y = - x² , y responda:
¿Cuál es el valor de a? ___________
El vértice se encuentra en el punto (_____,_____)
La concavidad es ________________
Las ramas abren ________________
El eje de simetría es X = __________
Tiene un valor máximo ó mínimo _______________
Realiza las observaciones que tengas con respecto a las dos graficas. ________________________________________________________________________________________________________________________________________________
ACTIVIDAD 4
FUNCIÓN CUADRÁTICA Y FUNCIÓN LINEAL
En GEOGEBRA realiza los siguientes gráficos en un solo sistema de coordenadas cartesianas:
1) y = x² y y = x (en entrada introduce primero y = x² el cuadrado lo puedes poner con la barra siguiente de entrada, y después y = x) con ayuda de la hoja de cálculo realiza las tablas y realiza los gráficos por separado para obtener el comportamiento de cada tabla.
2) y = x² +1 y y = x + 1 realiza lo mismo que en el inciso anterior.
Ahora realiza las observaciones en cuanto al comportamiento de cada grafico y la diferencia que existe en cada una de las tablas que obtuviste.
Observaciones tabla 1 y = x² y y = x
________________________________________________________________________________________________________________________________________________
Observaciones tabla 2 y = x² + 1 y y = x + 1
________________________________________________________________________________________________________________________________________________
ACTIVIDAD 5
RAICES DE LA ECUACIÓN CUADRÁTICA ASOCIADA A LA FUNCIÓN CUADRÁTICA
La grafica de una función cuadrática permite encontrar de forma visual la solución de la ecuación cuadrática.
Con ayuda de la hoja de cálculo obtén la tabla de valores y la grafica de las siguientes funciones cuadráticas:
f(x) = x² + 2x -8
g(x) = x² - 3x -10
Observa que cada grafica intercepta al eje x en dos puntos Indica el valor de cada punto:
x_1= __________ y x_2=__________
x_1= __________ y x_2=__________
Esos valores son las raíces o soluciones de cada una de las funciones cuadráticas anteriores.
Con ayuda de GEOGEBRA determina las raíces de las siguientes funciones cuadráticas y señale las raíces en el grafico.
f(x) = x² + 3x -10 x_1= ______ y x_2=_______
g(x) = x² + 2x +1 x_1= ______ y x_2= ______
h(x) = x² - x – 30 x_1= ______ y x_2= ______
k(x) = x² + 2x + 3 x_1= ______ y x_2= ______
ACTIVIDAD 6
ANALISIS DE COMPORTAMIENTO DE PARÁMETROS DE LA FUNCIÓN CUADRÁTICA
En un mismo sistema de coordenadas cartesianas realiza la grafica de las siguientes funciones y anota tus observaciones comparando las con x².
y = x² , y =5 x² y y = ¼ x²
Observaciones: ________________________________________________________________________________________________________________________________________________
Ahora realiza lo mismo pero con y = x²+5, y = x²-5 y compara con la grafica de y = x².
Observaciones: ________________________________________________________________________________________________________________________________________________
Realice los mismo pero ahora con y = (x+3)² y y = (x-3)² comparando las una vez más con y = x².
Observaciones: ________________________________________________________________________________________________________________________________________________
ACTIVIDAD 7
VERTICE DE UNA PARABOLA
El vértice de una parábola se representa por V (h, k), y se puede obtener algebraicamente y gráficamente.
Algebraicamente
Sabemos que las funciones cuadráticas se escriben de la forma general y=ax²+bx+c y se puede obtener fácilmente por el método de completar el trinomio cuadrado perfecto para poder expresarlo de la forma estándar y=a(x-h)²+k.
Gráficamente
Con ayuda de GEOGEBRA se puede graficar una función cuadrática y señalar el vértice.
Determina el vértice de la función f(x) = x² - 4x + 1 mediante el método de completar cuadrados y después verifica tu resultado con ayuda de GEOGEBRA señalando el lugar del vértice.
Si sabemos que h= (- b/2a) y que k= c - (b²/4a) se pueden aplicar estas formulas para obtener el vértice.
Determina el vértice de y = x² -2x + 3, si sabemos que a=_____, b=______ y c=______. Entonces aplicamos las fórmulas:
V (- b/2a , c - (b²/4a)
V (- _____/2_______ , _______ - (_____²/4_______))
V(-______, 3-______)
V(______,2)
Determina el vértice de las parábolas por uno de los dos métodos y comprueba tu resultado en GEOGEBRA.
f(x) = x² + 6x + 7
g(x) = x² - 6x + 13
h(x) = x² + 4 x + 1
ACTIVIDAD 8
Determina las características de la función cuadrática h(x) = - x²+ 2x - 4 si su vértice es V (1,-3) con ayuda de GEOGEBRA.
Coeficiente del término cuadrático_______________
Hacia donde abren las ramas_____________________
La concavidad es_______________________________
Se tienen un máximo o un mínimo_________________
El valor del máximo o mínimo es__________________
La ecuación de eje de simetría es x=h, entonces el eje de simetría es x=__________
El valor que corresponde al máximo o mínimo no los proporciona el valor de k.
Esto es f (h) = k por lo tanto vale _________.
ACTIVIDAD 9
Realiza un informe completo de gráficos y actividades y después envía por correo electrónico.
ACTIVIDADES A DESARROLLAR
Investigar diferentes conceptos de función
La creación de un libro ayudara al alumno a comprender un poco más el tema de funciones cuadráticas y podrá desarrollar un conocimiento más de cómo realizar un libro digital en la red.
Libro
Con la información encontrada en la investigación de conceptos de función, tanto impresa como digital. Los alumnos desarrollaran un libro digital.
Descripción de la actividad
Los alumnos desarrollaran un libro digital con los conceptos investigados (claro deberán agregar bibliografía de la fuente en donde encontraron la información en formato APA). Se les proporcionara un a liga en donde podrán ver como se hace un libro digital. Si llegan a tener alguna duda podrán publicar el muro de FACEBOOK algún comentario o duda.
Documentos extra
http://www.youtube.com/watch?v=7Rw20MLyOwk&feature=player_embedded
Situaciones que dan origen a funciones cuadráticas.
Los alumnos participaran en un foro para poder darse cuenta de las opiniones que tienen sus demás compañeros y poder interactuar con ellos vía un foro de debate para poder complementar su aprendizaje.
Foro
El alumno participara en el foro para analizar ejemplos que involucren funciones cuadradas.
Descripción de la actividad
Se propondrán algunos ejemplos que involucren diferentes tipos de funciones, en los cuales los alumnos tendrán que decir si involucran o no una función cuadrática. Si lo es proponer una forma de resolverlo. Al menos tendrán que tener una participación en cada propuesta.
Video: “Aplicación de la función cuadrática” http://www.youtube.com/watch?v=TF2_IjxOtyY consultado el 13 de agosto del 2010.
Paquete de ejercicios que involucran funciones cuadráticas.
Comparación de una función cuadrática con una función lineal.
Los alumnos desarrollaran una tarea en base a un software especializado para desarrollar graficas y poder hacer sus propias conclusiones en cuanto a la actividad desarrollada.
Tarea
El alumno analizara la grafica de una función cuadrática y la comparara con la grafica de una función lineal.
Descripción de la actividad
El alumno con ayuda de GEOGEBRA realizara las gráficas de una función cuadrática y una función lineal. Analizara las diferencias y realizara observaciones de los gráficos y las tablas que llevan al grafico.
Documentos extra
Serie de ejercicios clase
http://docentes.educacion.navarra.es/msadaall/geogebra/videos/index.htm
Intersecciones de la gráfica de una función cuadrática con el eje x.
En esta actividad se desea involucrar al alumno con las formas en que puede aparecer una función cuadrática y realizara sus conclusiones en cuanto que factores realizan cambios en cada grafica.
Tarea
Analizar las intersecciones de una función cuadrática con el eje de las abscisas.
Descripción de la actividad
El alumno con ayuda de GEOGEBRA graficara diferentes ejemplos de funciones cuadráticas. Interpretara el significado de esas intersecciones. Realizara un informe, en el cual exprese sus resultados después de graficar en GEOGEBRA.
Documentos extra
Serie ejercicios clase.
http://www.youtube.com/watch?v=In3qLE1E_II
Estudio gráfico y analítico de la función y=ax^2+bx+c, casos particulares:
y=ax^2,
y=ax^2+c,
y=a(x-h)^2,
y=a(x-h)^2+k.
El alumno desarrollara previamente ejercicios para identificar los valores que generan un cambio y los elementos que componen una función cuadrática. Con ello analizaran y podrán hacer sus conclusiones y comentarios.
Tarea
El alumno analizara las diferentes formas que se puede presentar una función cuadrática.
Descripción de la actividad
Con ayuda de GEOGEBRA el alumno graficara las funciones cuadrática que se presenten en la actividad y realizaran sus observaciones del comportamiento de cada una.
Después de la clase presencial el alumno será capaz de resolver funciones cuadráticas realizando despejes, factorizaciones, completando el trinomio cuadrado perfecto o formula general.
Por lo tanto también presentara un informe con sus procedimientos y resultados.
Concavidad, máximo o mínimo.
Con los análisis realizados en la actividad anterior los alumnos comprenderán y analizaran los componentes de una parábola (grafica de una función cuadrática) y podrán determinar sin su grafica cada uno de estos componentes.
Tarea
El alumno analizara cada uno de los elementos de una función cuadrática.
Descripción de la actividad
El alumno investigara en un libro los procedimientos para encontrar la concavidad, el vértice, el eje de simetría y el máximo o mínimo de una función cuadrática.
Con ayuda de GEOGEBRA localizara cada una de estas características de diferentes funciones cuadráticas y realizara sus observaciones.
Realizara un informe de procedimientos para calcular tales elementos.
Evaluación
Se realizara una evaluación esperando que el alumno plasme los conocimientos adquirido mediante un cuestionario que evaluara dichos conocimientos desarrollados en las actividades realizadas anteriormente.
Cuestionario
Analizar los conocimientos adquiridos en la unidad.
Descripción de la actividad
El alumno entrara a la plataforma para realizar el cuestionario llamado “Función Cuadrática”.
Instrucciones:
Hacer clic en el cuestionario “función Cuadrática”.
Cuando aparezca en la pantalla hacer clic en el botón “pre visualizar el cuestionario ahora”.
Cuando se despliegue el cuestionario, responder cuidadosamente cada una de las preguntas, al finalizar hacer clic en el botón “Enviar todo y terminar”.
Este cuestionario es individual.
BIBLIOGRAFÍA DE CONSULTA PARA EL PROFESOR Raymond A. Barnett (1984). ALGEBRA (Primera edición en español). (Capitulo 11.3 Gráfica de funciones lineales y cuadráticas página 338-347). México: McGraw-Hill.
La Función cuadrática. Parábolas. (Ministerio de Educación. Año 2001). Pagina web Recursos Tic Educación (Descartes 2D):
http://recursostic.educacion.es/descartes/web/materiales_didacticos/Funcion_cuadratica_parabola/index.htm
Ejemplos diversos de webs interactivas de Matemáticas. Diseñadas con GeoGebra por Manuel Sada Allo. Manuel Sada Allo (2005-10)
http://docentes.educacion.navarra.es/msadaall/geogebra/index.htm
TAREA OPERATIVO DÍA DE MUERTOS 2010
Lo siento mucho pero la tarea estara disponible en el grupo de trabajo CCH AZCAPO VICTOR OLIVA dentro de GOOGLE Grupos que ya les habia mencionado de clic en la siguiente liga y llegara al grupo. Las tareas estaran etiquetadas por tarea unidad 4. (Esto fue por cuestiones de formato).
TAREA
TAREA
viernes, 22 de octubre de 2010
Integración paso a paso
Forma paso a paso y directa.
Ahora se llama otra biblioteca with(Student[Calculus1] y el comando infolevel[calculus1], que nos ayudara a resolverlo paso a paso, y showsteps() junto con IntTutor(función, con respecto a quien se integra) que la realiza abriendo una ventana extra en donde se oprime next step que presenta paso a paso o all steps y aparecen todos los pasos, que se pueden pegar en word o en un presentación.
> restart;
> with(Student[Calculus1]);
> infolevel[Calculus1] := 1;
> Int(1/(x*(x^2+1)^2), x);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
>
> ShowSteps();
> IntTutor(1/(x*(x^2+1)^2), x);
Ahora se llama otra biblioteca with(Student[Calculus1] y el comando infolevel[calculus1], que nos ayudara a resolverlo paso a paso, y showsteps() junto con IntTutor(función, con respecto a quien se integra) que la realiza abriendo una ventana extra en donde se oprime next step que presenta paso a paso o all steps y aparecen todos los pasos, que se pueden pegar en word o en un presentación.
> restart;
> with(Student[Calculus1]);
> infolevel[Calculus1] := 1;
> Int(1/(x*(x^2+1)^2), x);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
> Hint(%);
> Rule[%](`%%`);
>
> ShowSteps();
> IntTutor(1/(x*(x^2+1)^2), x);
Integración varias
Para integrar esto primero se completa el trinomio cuadrado perfecto con el comando completesquare(sedefine la función), definiendola como f1.
> restart; with(student);
> f := 1/sqrt(10+3*x-(1/4)*x^2);
> f1 := completesquare(10+3*x-(1/4)*x^2);
> Int(1/f1^(1/2), x);
> Int(f, x) = value(%)+c;
> Int(f, x) = int(f, x);
Para integrar por partes se llama a la biblioteca with(student) que ya se venia manejando en ejercicios anteriores, se define la integral con Int(función, variable), se ocupa el comando intparts(integral de la función, parte a separar), simplify simplifica el resultado, value resuelve la integral restante y factor factoriza el resultado si se pudiera factorizar y se le agrega la constate de integración.
> restart; with(student);
> p1 := Int(x*ln(x), x);
> p2 := intparts(p1, ln(x));
> p3 := simplify(p2);
> p4 := value(p3);
> p5 := factor(p4);
> p1 = p5+c;
En forma directa.
> Int(x*ln(x), x) = int(x*ln(x), x)+c;
Por partes trigonométricas inversas
> restart;
> with(student);
> p1 := Int(arctan(sqrt(2*x)), x);
> p2 := intparts(p1, arctan(sqrt(2*x)));
> p3 := op(2, p2);
> p4 := changevar(sqrt(2*x) = u, p3, u);
> p5 := eval(value(p4), u = sqrt(2*x))+c;
> p1 = op(1, p2)+p5;
> En forma directa se tiene(como texto);
> Int(arctan(sqrt(2*x)), x) = int(arctan(sqrt(2*x)), x)+c;
> restart; with(student);
> f := 1/sqrt(10+3*x-(1/4)*x^2);
> f1 := completesquare(10+3*x-(1/4)*x^2);
> Int(1/f1^(1/2), x);
> Int(f, x) = value(%)+c;
> Int(f, x) = int(f, x);
Para integrar por partes se llama a la biblioteca with(student) que ya se venia manejando en ejercicios anteriores, se define la integral con Int(función, variable), se ocupa el comando intparts(integral de la función, parte a separar), simplify simplifica el resultado, value resuelve la integral restante y factor factoriza el resultado si se pudiera factorizar y se le agrega la constate de integración.
> restart; with(student);
> p1 := Int(x*ln(x), x);
> p2 := intparts(p1, ln(x));
> p3 := simplify(p2);
> p4 := value(p3);
> p5 := factor(p4);
> p1 = p5+c;
En forma directa.
> Int(x*ln(x), x) = int(x*ln(x), x)+c;
Por partes trigonométricas inversas
> restart;
> with(student);
> p1 := Int(arctan(sqrt(2*x)), x);
> p2 := intparts(p1, arctan(sqrt(2*x)));
> p3 := op(2, p2);
> p4 := changevar(sqrt(2*x) = u, p3, u);
> p5 := eval(value(p4), u = sqrt(2*x))+c;
> p1 = op(1, p2)+p5;
> En forma directa se tiene(como texto);
> Int(arctan(sqrt(2*x)), x) = int(arctan(sqrt(2*x)), x)+c;
Integración directa
> f := 1/(1+sin(3*x));
> Int(f, x) = int(f, x);
> f := 4/(x^2+2);
> Int(f, x) = int(f, x);
> f := 2/(5*x^2-8);
> Int(f, x) = int(f, x);
> f := sqrt(5-x^2);
> Int(f, x) = int(f, x);
Como en la derivada ahora se maneja el comando Int(f,x) para definir la función y int(f,x) para integrar.
> Int(f, x) = int(f, x);
> f := 4/(x^2+2);
> Int(f, x) = int(f, x);
> f := 2/(5*x^2-8);
> Int(f, x) = int(f, x);
> f := sqrt(5-x^2);
> Int(f, x) = int(f, x);
Como en la derivada ahora se maneja el comando Int(f,x) para definir la función y int(f,x) para integrar.
Variación de crecimiento de área
> restart; with(difforms); with(student);
> defform(f = 0, w1 = 1, w2 = 1, w3 = 1, v1 = 1, x = 0, y = 0, z = 0, t = 0, a = const, b = const, e = const, c = const);
> A(l):=l^(3);#`Fórmula del área de un cuadrado.`;
> f := proc (x) options operator, arrow; x^3 end proc;
> dy = d(f(x));
> subs([x = 5, d(x) = 0.2e-2], %);
> defform(f = 0, w1 = 1, w2 = 1, w3 = 1, v1 = 1, x = 0, y = 0, z = 0, t = 0, a = const, b = const, e = const, c = const);
> A(l):=l^(3);#`Fórmula del área de un cuadrado.`;
> f := proc (x) options operator, arrow; x^3 end proc;
> dy = d(f(x));
> subs([x = 5, d(x) = 0.2e-2], %);
Formas Diferenciales
> restart; with(difforms);
> defform(f = 0, w1 = 1, w2 = 1, w3 = 1, v1 = 1, x = 0, y = 0, z = 0, t = 0, a = const, b = const, e = const, c = const);
> dy = d(x^2);
> dy = d(3*x^2+5*x);
> dy = d(sqrt(1-3*x));
> f := x^3-y^2 = 3*x-4;
> dy/dx = implicitdiff(f, y, x);
> %*dx;
> sort(%);
> d(x^3-y^2 = 3*x-4);
> isolate(%, d(y));
> simplify(%);
> sort(%);
> f := 4*x^5-5*x^2-1;
> d^3*y/dx^3 = diff(f, `$`(x, 3));
> %*dx^3;
> sort(%);
solución 2 Usando la forma de diferencial.
> dy = d(4*x^5-5*x^2-1);
> d^2*y = d(20*x^4-10*x)*d(x);
> d^3*y = d(80*x^3-10)*d(x)^2;
> defform(f = 0, w1 = 1, w2 = 1, w3 = 1, v1 = 1, x = 0, y = 0, z = 0, t = 0, a = const, b = const, e = const, c = const);
> dy = d(x^2);
> dy = d(3*x^2+5*x);
> dy = d(sqrt(1-3*x));
> f := x^3-y^2 = 3*x-4;
> dy/dx = implicitdiff(f, y, x);
> %*dx;
> sort(%);
> d(x^3-y^2 = 3*x-4);
> isolate(%, d(y));
> simplify(%);
> sort(%);
> f := 4*x^5-5*x^2-1;
> d^3*y/dx^3 = diff(f, `$`(x, 3));
> %*dx^3;
> sort(%);
solución 2 Usando la forma de diferencial.
> dy = d(4*x^5-5*x^2-1);
> d^2*y = d(20*x^4-10*x)*d(x);
> d^3*y = d(80*x^3-10)*d(x)^2;
miércoles, 20 de octubre de 2010
FORMAS DIFERENCIALES
Formas diferenciales
> restart; with(difforms);
> defform(f = 0, w1 = 1, w2 = 1, w3 = 1, v1 = 1, x = 0, y = 0, z = 0, t = 0, a = const, b = const, e = const, c = const);
> dy = d(x^2);
> dy = d(3*x^2+5*x);
> dy = d(sqrt(1-3*x));
> f := x^3-y^2 = 3*x-4;
> dy/dx = implicitdiff(f, y, x);
> %*dx;
> sort(%);
> d(x^3-y^2 = 3*x-4);
> isolate(%, d(y));
> simplify(%);
> sort(%);
> f := 4*x^5-5*x^2-1;
> d^3*y/dx^3 = diff(f, `$`(x, 3));
> %*dx^3;
> sort(%);
solución 2 Usando la forma de diferencial.
> dy = d(4*x^5-5*x^2-1);
> d^2*y = d(20*x^4-10*x)*d(x);
> d^3*y = d(80*x^3-10)*d(x)^2;
> restart; with(difforms);
> defform(f = 0, w1 = 1, w2 = 1, w3 = 1, v1 = 1, x = 0, y = 0, z = 0, t = 0, a = const, b = const, e = const, c = const);
> dy = d(x^2);
> dy = d(3*x^2+5*x);
> dy = d(sqrt(1-3*x));
> f := x^3-y^2 = 3*x-4;
> dy/dx = implicitdiff(f, y, x);
> %*dx;
> sort(%);
> d(x^3-y^2 = 3*x-4);
> isolate(%, d(y));
> simplify(%);
> sort(%);
> f := 4*x^5-5*x^2-1;
> d^3*y/dx^3 = diff(f, `$`(x, 3));
> %*dx^3;
> sort(%);
solución 2 Usando la forma de diferencial.
> dy = d(4*x^5-5*x^2-1);
> d^2*y = d(20*x^4-10*x)*d(x);
> d^3*y = d(80*x^3-10)*d(x)^2;
REPRESENTACIÓN GRAFICA DE LA DERIVADA
restart:with(plots):f:=x->root[3](x);
> f(x+h);
> f(x+h)-f(x);
> %/h;
> Limit(%,h=0,right):%=value(%);
> Limit((f(x)-f(x-h))/h,h=0,left):%=value(%);
> p1:=plot(f(x),x=-0.5..4,y=-4..2,color=blue,thickness=3):
> p2:=plot(rhs(%%),x=-0.5..4,y=-2..2,color=brown,thickness=3):
> display(p1,p2);
>
> f(x+h);
> f(x+h)-f(x);
> %/h;
> Limit(%,h=0,right):%=value(%);
> Limit((f(x)-f(x-h))/h,h=0,left):%=value(%);
> p1:=plot(f(x),x=-0.5..4,y=-4..2,color=blue,thickness=3):
> p2:=plot(rhs(%%),x=-0.5..4,y=-2..2,color=brown,thickness=3):
> display(p1,p2);
>
DERIVADAS CON MAPLE 13 (Taller de MAPLE ACATLAN)
restart:#Derivadas de funciones directasf:=x->x^3;
> Diff(f(x),x)=diff(f(x),x);#Diff es el comando para derivar.
> Diff(f(x),x$2)=diff(f(x),x$2);#Segunada derivada se agrega $2.
> Diff(f(x),x$3)=diff(f(x),x$3);#Tercera derivada se agrega $3 y asi sucesivamente.
> Diff(f(x),x$4)=diff(f(x),x$4);#Derivada de orden n.
> restart:
> f:=x->x^4-2*x+5*x+7;
> Diff(f(x),x)=diff(f(x),x);
> Diff(f(x),x$2)=diff(f(x),x$2);
> Diff(f(x),x$3)=diff(f(x),x$3);
> Diff(f(x),x$4)=diff(f(x),x$4);
> Diff(f(x),x$5)=diff(f(x),x$5);
> restart:
> f:=x->(3-x)*(2+x);
> expand(f(x));#Realiza el producto.
> factor(%);#factor: Factoriza la expresión anterior.
> Diff(%,x)=diff(%,x);
> restart:
> f:=x->3/x^2;
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sqrt(x)+1/sqrt(x);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->(x^3-1)/(x+5);
> Diff(f(x),x)=diff(f(x),x);
> factor(%);
> restart:
> f:=x->root[3](x+1)^4;#root[3]= raíz cubica.
> Diff(f(x),x)=diff(f(x),x);
> restart:
> x:=(y^2-7)^2;
> 1/Diff(x,y)=1/diff(x,y);
> restart:
> x:=root[3](5-y^2);#Para resolver raices enecimas se cambia root[n]
> 1/Diff(x,y)=1/diff(x,y);
> restart:
> f:=x->sin(a*x);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sin(3*x^2-1);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sin(x/2)^2:
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->root[3](tan(2*x));
> Diff(f(x),x)=diff(f(x),x);
> simplify(%,'symbolic');
> restart:
> f:=x->sin(tan(x));#Funciones trigonometricas explisitas
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sec(cos(10*x)^2);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->arcsin(5*x^2);#arcsin, es la función del arco seno
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->arccos(x/2);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->arccsc(2*x);
> Diff(f(x),x)=diff(f(x),x);
> simplify(%,'symbolic');
> restart:
> f:=x->arcsin(sqrt(tan(x)));
> Diff(f(x),x)=diff(f(x),x);
> restart:#Derivada de logaritmos
> f:=x->log[10](3/x);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->ln(a*x+3);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->ln(ln(x));
> Diff(f(x),x)=diff(f(x),x);
> restart:#Derivadas de exponenciales
> f:=x->10^(x^2+5*x-6);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->x^x;
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->x^(2*x);
> Diff(f(x),x)=diff(f(x),x);
> factor(%);
> simplify(%,'symbolic');
> restart:
> f:=x->sqrt(ln(sec(sqrt(x))));
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->exp(10^(root[3](sin(x))));
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->(sec(x)*tan(x)^3)^cos(x);
> Diff(f(x),x)=diff(f(x),x);
> factor(%);
> restart:#Derivada de una función de funciones
> F:=u->u^3;G:=u->(2*x+1)/4;
> Diff('F(G(x))',x)=diff(F(G(u)),x);
> simplify(%);
> restart:
> f:=x->x^2-8*x-3;
> g:=x->x^2+1;
> diff((f@g)(x),x);
> expand(%);
> restart:#derivadas de funciones paramétricas
> f:=a*cos(theta)=x;
> g:=b*sin(theta)=y;
> dy/dx=implicitdiff({f,g},{y,theta},y,x);
> subs(-b*cos(thetha)/a*sin(theta)=-b/a*tan(theta),%);
> #Obteniendo la segunda derivada
> 'd^2*y/dx^2'=implicitdiff({f,g},{y,theta},y,x$2);
> 'd^2*y/dx^2'=simplify(-b*(sin(theta)^2+cos(theta)^2)/a^2/sin(theta)^3,'symbolic');
> subs(-b/a^2/sin(theta)^3=-b/a^2*csc(theta)^3,%);
> Diff(f(x),x)=diff(f(x),x);#Diff es el comando para derivar.
> Diff(f(x),x$2)=diff(f(x),x$2);#Segunada derivada se agrega $2.
> Diff(f(x),x$3)=diff(f(x),x$3);#Tercera derivada se agrega $3 y asi sucesivamente.
> Diff(f(x),x$4)=diff(f(x),x$4);#Derivada de orden n.
> restart:
> f:=x->x^4-2*x+5*x+7;
> Diff(f(x),x)=diff(f(x),x);
> Diff(f(x),x$2)=diff(f(x),x$2);
> Diff(f(x),x$3)=diff(f(x),x$3);
> Diff(f(x),x$4)=diff(f(x),x$4);
> Diff(f(x),x$5)=diff(f(x),x$5);
> restart:
> f:=x->(3-x)*(2+x);
> expand(f(x));#Realiza el producto.
> factor(%);#factor: Factoriza la expresión anterior.
> Diff(%,x)=diff(%,x);
> restart:
> f:=x->3/x^2;
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sqrt(x)+1/sqrt(x);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->(x^3-1)/(x+5);
> Diff(f(x),x)=diff(f(x),x);
> factor(%);
> restart:
> f:=x->root[3](x+1)^4;#root[3]= raíz cubica.
> Diff(f(x),x)=diff(f(x),x);
> restart:
> x:=(y^2-7)^2;
> 1/Diff(x,y)=1/diff(x,y);
> restart:
> x:=root[3](5-y^2);#Para resolver raices enecimas se cambia root[n]
> 1/Diff(x,y)=1/diff(x,y);
> restart:
> f:=x->sin(a*x);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sin(3*x^2-1);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sin(x/2)^2:
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->root[3](tan(2*x));
> Diff(f(x),x)=diff(f(x),x);
> simplify(%,'symbolic');
> restart:
> f:=x->sin(tan(x));#Funciones trigonometricas explisitas
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->sec(cos(10*x)^2);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->arcsin(5*x^2);#arcsin, es la función del arco seno
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->arccos(x/2);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->arccsc(2*x);
> Diff(f(x),x)=diff(f(x),x);
> simplify(%,'symbolic');
> restart:
> f:=x->arcsin(sqrt(tan(x)));
> Diff(f(x),x)=diff(f(x),x);
> restart:#Derivada de logaritmos
> f:=x->log[10](3/x);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->ln(a*x+3);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->ln(ln(x));
> Diff(f(x),x)=diff(f(x),x);
> restart:#Derivadas de exponenciales
> f:=x->10^(x^2+5*x-6);
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->x^x;
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->x^(2*x);
> Diff(f(x),x)=diff(f(x),x);
> factor(%);
> simplify(%,'symbolic');
> restart:
> f:=x->sqrt(ln(sec(sqrt(x))));
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->exp(10^(root[3](sin(x))));
> Diff(f(x),x)=diff(f(x),x);
> restart:
> f:=x->(sec(x)*tan(x)^3)^cos(x);
> Diff(f(x),x)=diff(f(x),x);
> factor(%);
> restart:#Derivada de una función de funciones
> F:=u->u^3;G:=u->(2*x+1)/4;
> Diff('F(G(x))',x)=diff(F(G(u)),x);
> simplify(%);
> restart:
> f:=x->x^2-8*x-3;
> g:=x->x^2+1;
> diff((f@g)(x),x);
> expand(%);
> restart:#derivadas de funciones paramétricas
> f:=a*cos(theta)=x;
> g:=b*sin(theta)=y;
> dy/dx=implicitdiff({f,g},{y,theta},y,x);
> subs(-b*cos(thetha)/a*sin(theta)=-b/a*tan(theta),%);
> #Obteniendo la segunda derivada
> 'd^2*y/dx^2'=implicitdiff({f,g},{y,theta},y,x$2);
> 'd^2*y/dx^2'=simplify(-b*(sin(theta)^2+cos(theta)^2)/a^2/sin(theta)^3,'symbolic');
> subs(-b/a^2/sin(theta)^3=-b/a^2*csc(theta)^3,%);
martes, 19 de octubre de 2010
Tarea Mate 1 UNIDAD 3 - 5

UNIVERSIDAD NACIONAL AUTONOMA DE MÉXICO
COLEGIO DE CIENCIAS Y HUMANIDADES
PLATEL AZCAPOTZALCO
MATEMATICAS 1 UNIDAD 3 Tarea 5
PROBLEMAS DE VELOCIDAD, TIEMPO Y DISTANCIA
1.- Un tren carguero sale de Guadalajara hacia Tepic a 40 km⁄h. Dos horas después un tren de pasajeros sale de la misma estación hacia Tepic viajando a 60 km⁄h. ¿Cuánto tarda el tren de pasajeros en alcanzar al carguero?
2.- Dos aviones parten del Distrito Federal a las 10 am, uno se dirige a Brasil a 960 km⁄h y otro en dirección contraria a 240 km⁄h. ¿En qué momento estarán separados 1500 km? ¿Qué distancia a recorrido cada uno?
3.- Juan y José fueron en un viaje de campamento con sus motocicletas. Un día por la mañana José dejo el campamento y viajo en su motocicleta rumbo al pueblo para comprar víveres. Veinte minutos después Juan decidió ir también, si José viajo a 50 km⁄h y Juan lo hizo a 40 km⁄h. ¿Qué tiempo tardo Juan en alcanzar a José?
4.- Un carro sale del Distrito Federal hacia Veracruz viajando con una velocidad promedio de 90 km⁄h. Al mismo tiempo, otro carro sale de Veracruz hacia el Distrito Federal a 80 km⁄h. Si entre las dos ciudades hay una distancia aproximada de 415 km. ¿Cuánto tardaran en encontrase los dos carros, suponiendo que los dos conserven dicha velocidad?
5.- Una patrulla de caminos localiza un coche que va con exceso de velocidad a 120 km⁄h y que lleva una ventaja de 0.8 km. Si la patrulla baja con velocidad media de 150 km⁄h. ¿Cuánto tardara en alcanzar al coche?
PROBLEMAS DE MEZCLAS
1.- Un granjero desea mezclar leche que contenga 3 % de grasa con crema que contenga 30 % de grasa para obtener 900 litros de leche, que contenga 8% de grasa. ¿Qué cantidad debe de usar de cada producto?
2.- Un comerciante desea mezclar dos tipos de frijol, uno de los cuales se vende a $ 32.00, el kilogramo y otro a $ 32.80, el kilogramo. Si pone 25 kilogramos de $ 32.00. ¿Qué cantidad de frijol de $ 32.80 debe de agregar en la mezcla para que el costo final de la mezcla total sea equivalente al precio de $ 32.20, el kilogramo?
3.- Se mezclan cuarenta litros de un insecticida al 60 % con una solución al 10 % para tener una solución al 20 %. ¿Cuánta solución al 10 % debe usarse?
4.- Un doctor ordena 20 gramos de una solución al 52 % de cierta medicina. El boticario tiene solo frascos de solución al 40 % y al 70 %. ¿Cuánto de cada frasco debe usarse para surtir la receta?
5.- Un administrador una tienda desea reducir los precios en un grano de café fresco mezclando dos tipos de granos. Si tiene 50 kilogramos de café que vende a $ 120.00 el kilogramo. ¿Cuánto del grano de $ 80.00 el kilogramo debe mezclar debe mezclar para que pueda vender a $ 100.00 el kilogramo de la mezcla?
PROBLEMAS DE EDADES
1.- La edad del padre de María es el cuádruple de la de ella. Hace 5 años, su edad era siete veces la de su hija. ¿Cuál es la edad actual de cada uno?
2.- Ana es seis años mayor que Juan. Hace seis años ella tenía el doble de la edad de él. ¿Qué edad tiene cada uno actualmente?
3.- El papa de Salvador es 26 años mayor que él. Dentro de 10 años la suma de sus edades será 80. ¿Cuáles son sus edades actuales?
4.- La edad de Karla es el doble de la de Susana. Si restamos 8 a la edad de Susana y sumamos 4 a la de Karla, Karla tendrá entonces 4 veces la edad de Susana. ¿Cuáles son sus edades actuales?
6.- Laura es 8 años mayor que Claudia. Hace 20 años la edad de Laura era el triple de la de Claudia. ¿Qué edad tiene cada una?
PROBLEMAS DE FINANZAS
1.- Germán invirtió $ 10,000.00. Una parte la metió al banco al 5 % de interés, el resto lo metió en bonos por el que pagan 9 % de rendimiento anual. ¿Cuánto invirtió en cada parte si al año su ganancia por las dos inversiones fue de $ 660.00?
2.- El Señor Pineda invirtió $ 50,000.00, parte al 6 % y parte al 8 %. El interés anual de la inversión al 6 %fue de $ 480.00 más que la inversión al 8 %. ¿Cuánto invirtió en cada tasa?
lunes, 18 de octubre de 2010
Tarea Mate 1 UNIDAD 3 - 4

UNIVERSIDAD NACIONAL AUTONOMA DE MÉXICO
COLEGIO DE CIENCIAS Y HUMANIDADES
PLATEL AZCAPOTZALCO
MATEMATICAS 1 UNIDAD 3 Tarea 4
Resuelva los siguientes problemas numéricos:
1.- Hay dos números cuya suma es cincuenta. El triple del primero es cinco unidades mayor que el doble del segundo. ¿Cuáles son dichos números?
2.- Encuentra tres enteros pares consecutivos tales que el mayor sea el triple del menor.
3.- Hay tres enteros impares consecutivos. El triple del mayor es siete veces el menor. ¿Cuáles son los números?
4.- En un triángulo rectángulo, la hipotenusa es 3 cm más larga que el cateto mayor. Si el cateto menor mide 3 cm. ¿Cuánto miden los otros lados?
5.- Un hombre hace un trabajo en tres días, el mismo trabajo su hijo lo hace en seis días, si trabajan juntos tanto el hombre como su hijo. ¿Cuánto tiempo tardarían en realizar el mismo trabajo?
6.- Hay tres enteros consecutivos. La suma de los dos primeros es 35 unidades mayor que el tercero. Encuentra los números.
7.- Hay un número tal que tres veces el número menos 6 es igual a 45. Encuentra el número.
8.- El primer lado de un triángulo es 2 cm menor que el segundo. Si el perímetro del triángulo es 33 cm. ¿Qué longitud tiene cada lado?
9.- Una llave puede llenar un tanque de agua en 4 minutos y otra llenarlo en 5 minutos. ¿En cuánto tiempo se llena el tanque si se abren ambas llaves?
10.- El área de un triangulo isósceles es de 48 〖cm〗^2, si su altura mide 8 cm. ¿Cuánto mide la base? ¿Cuánto mide el perímetro del triángulo?
sábado, 16 de octubre de 2010
TAREA MATE 1 UNIDAD 3 - 3

UNIVERSIDAD NACIONAL AUTONOMA DE MÉXICO
COLEGIO DE CIENCIAS Y HUMANIDADES
PLATEL AZCAPOTZALCO
MATEMATICAS 1 UNIDAD 3 Tarea 3
Determinar la pendiente y las intersecciones con los ejes coordenados de cada una de las siguientes rectas y realiza una grafica señalando la ordenada al origen y la solución o raíz de ecuación:
a) 3/5 x-y+1/2=0
b) 3x+y-2=0
c) -11x+6y-3=0
d) 1/6 x+2/9 y-1/3=0
e) 3/4 x+5y-12=0
f) 3x+5/3 y+8=0
g) 12x-3y+8=0
h) 4x+7y-28=0
i) -3x+5y+15=0
j) 2x-20y=5
k) 5x+8y=6
l) x-y-5=0
m) -3/4 x+2/5 y=1/2
n) 2/3+4/3 y-7/3 x=0
0) -4x+5=y
En los siguientes ejercicios de la forma ax+b=c, encuentra la coordenada x, cuando y=c, y realiza la gráfica.
a) y=2x+4, cuando y=6
b) y=-1/2 x-5/3, cuando y=13/3
c) y=x+5, cuando y=4
d) y=-3/4 x+7, cuando y=3
f) y=3x-3, cuando y=3
g) y=-3/4 x+6/5, cuando y=21/5
h) y=2x-2, cuando y=3
i) y=-3/4 x+7/2, cuando y=5/2
j) y=-5x+2, cuando y=9/7
k) y=5/6 x-3/7, cuando y=4
TAREA MATE 1 UNIDAD 3 - 2

UNIVERSIDAD NACIONAL AUTONOMA DE MÉXICO
COLEGIO DE CIENCIAS Y HUMANIDADES
PLATEL AZCAPOTZALCO
MATEMATICAS 1 UNIDAD 3 Tarea 2
Resuelva los siguientes reactivos:
Resuelva: d=vt, para v. (distancia velocidad tiempo).
Resuelva: d=1100t, para t. (Distancia, en pies, recorrida por el sonido).
Resuelva: C=2πr, para r. (Circunferencia de un círculo).
Resuelva: I=Prt, para t . (Interés simple).
Resuelva: C=πD, para π. (Circunferencia de un círculo).
Resuelva: e=mc^2, para m. (Ecuación-masa-energía).
Resuelva: ax+b=0, para x . (Ecuación polinomial de primer grado).
Resuelva: p=2a+2b, para a. (Perímetro de un rectángulo).
Resuelva: y=2x-5, para x. (Ecuación de una recta).
Resuelva: y=mx+b, para m. (Ecuación de una recta).
Resuelva: 3x-4y-12=0, para y. (Ecuación lineal, de dos variables).
Resuelva: I=E/R, para R. (Circuitos eléctricos, Ley de Ohm).
Resuelva: m=b/a, para a. (Óptica: amplificación).
Resuelva: C=100B/L, para B. (Antropología, índice cefálico).
Resuelva: (IQ)=(100(MA))/((CA)), para (CA). (Psicología: cociente intelectual).
Resuelva: F=9/5 C+32, para C. (Grados centígrados-Fahrenheit).
Resuelva: F=9/5 C+32, para C. (Grados centígrados-Fahrenheit).
Resuelva: 1/f=1/a+1/b, para f. (Óptica: Longitud focal).
Resuelva: 1/R=1/R_1 +1/R_2 , para R. (Circuitos eléctricos).
Resuelva: y=(3x+2)/(2x-4), para x. (Ecuación racional).
viernes, 8 de octubre de 2010
tarea 1 Mate 1 Unidad 3

UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
COLEGIO DE CIENCIAS Y HUMANIDADES
PLANTEL AZCAPOTZALCO
ING. VICTOR OLIVA
Resuelva las ecuaciones y verifique cada resultado.
x-7=-9
-8x=6
-4m+5=-9
2t+9=5t-6
2y+8=2y-6
5x+10(x-2)=40
x+4=-6
5x=-13
-5m=0
3y=0
6w+18=-2
3x-4=6x-19
4y+7=2y-6
3x-5=x+6
x-3=x+7
3(x+2)=5(x-6)
4(x-2)=4x-8
3y+6=3(y+2)
5+4(t-2)=2(t+7)+1
7x-(8x-4)-2=5-(4x+2)
10x+25(x−3)=275
x+(x+2)+(x+4)=54
5w-(7w-4)-2=5-(3w+2)
-3(4-t)=5-(t+1)
x(x-1)+5=x^2+x-3
x(x-4)-2=x^2-4(x+3)
x(x+2)=x(x+4)-12
t(t-6)+8=t^2-6t-3
-2{3+[2x-(x-4) ] }=2[(x+2)-3]
-2{2-[1-2(x+1) ] }=2(x+5)-4
¿Cuál de las siguientes ecuaciones es equivalente a 2x+5=x-3: 2x=x-8 , 2x=x+2 , 3x=12, x=-8?
Resuelva cada ecuación y verifique su resultado:
x/5-2= 3/5
x/3+x/6=4
m/4-m/3=1/2
x/7-1=1/7
y/4+y/2=9
n/5-n/6=6/5
5/12-m/3=4/9
2/3-x/8=5/6
.7x=21
0.9x=540
0.7x+0.9x=32
0.3x+0.5x=24
1/2-2/x=3/x
2/x-1/3=5/x
1/m-1/9=4/9-2/3m
1/2t+1/8=2/t-1/4
(x-2)/3+1=x/7
(x+3)/2-x/3=4
(2x-3)/9-(x+5)/6=(3-x)/2-1
(3x+4)/3-(x-2)/5=(2-x)/15-1
0.1(x-7)+0.05x=0.8
0.4(x+5)-0.3x=17
0.02x-0.5(x-2)=5.32
0.3x-0.04(x+1)=2.04
7/(y-2)-1/2=3
9/(A+1)-1= 12/(A+1)
3/(2x+1)+4=6x/(2x-1)
5x/(x+5)=2-25/(x+5)
2E/(E-1)=2+5/2E
3N/(N-2)-9/4N=3
(n-5)/(6n-6)=1/9-(n-3)/(4n-4)
1/3-(s-2)/(2s+4)=(s+2)/(3s+6)
5+ 2x/(x-3)=6/(x-3)
6/(x-2)=3+3x/(x-2)
(x^2+2)/(x^2-4)=x/(x-2)
5/(x-3)=(33-x)/(x^2-6x+9)
3x/24-(2-x)/10=(5+x)/40-1/15
2x/10-(3-x)/14=(2+x)/5-1/2
(5t-22)/(t^2-6t+9)-11/(t^2-3t)-5/t=0
1((x-33)/(x^2-6x+9))+5/(x-3)=0
5- 2x/(3-x)=6/(x-3)
3x/(2-x)+6/(x-2)=3
1/(c^2-c-2)-3/(c^2-2c-3)=1/(c^2-5c+6)
(5t-22)/(t^2-6t+9)-11/(t^2-3t)=5/t
miércoles, 6 de octubre de 2010
Secuencia Didáctica en Equipo
ACTIVIDADES
1. Los alumnos se organizaran en equipos de máximo 5 integrantes, cada equipo seleccionara un nombre y un jefe de equipo con el cual tendrán que crear:
• Una cuenta de correo electrónico en GMAIL
• Una cuenta en la red social FACEBOOK
• Un BLOG en BLOGSPOT.
El correo electrónico creado se enviara al profesor para integrarlo al grupo de trabajo creado en GOOGLE grupos con el nombre de CCH AZCAPÓ VICTOR OLIVA.
En este grupo subirán sus actividades con el nombre del equipo y numero de grupo al que pertenecen.
2. En FACEBOOK se subirá una foto de los integrantes del equipo edita en http://www.picnik.com/ y se mandara la liga o invitación a FACCEBOOK al profesor para ver dicha actividad, dicha foto también se publicara en el blog que ustedes crearon.
3. Investigación de conceptos de:
• Función y relación,
• Función Lineal,
• Grafica de una función lineal,
• Elementos de la grafica de una función lineal.
Foro
Los equipos participaran en el foro para analizar los conceptos anteriores.
Descripción de la actividad
Se investigaran en internet conceptos de función y relación, función lineal, grafica y elementos de una función lineal. Entraran a GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, y participaran en debates (foro) escribiendo las definiciones encontradas, si algún equipo encontró la misma que ustedes podrán a completar o describir algún ejemplo. Cada equipo tendrá como mínimo dos participaciones en el debate y incluirán una bibliografía o página de internet de donde y quien publica dicha definición o investigación.
4. Situación que describe un comportamiento lineal.
Tarea
Cada equipo buscara ejemplos en la vida cotidiana que describa el comportamiento de una variación lineal.
Descripción de la actividad
Los integrantes de cada equipo tendrán que discutir el problema propuesto y realizar un análisis de cómo desarrollarían el ejemplo para poder resolverlo. Podrán proponer las tres formas para representarlo. Trabajo se explicara en una cuartilla y se subirá a GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, en el área de archivos se subirá dicho trabajo (incluir una portada con los integrantes de cada equipo).
5. Propuesta solución hoja cálculo.
Tarea
El equipo resolverá dicho problema realizando una tabla de datos y graficara dichos elementos de la tabla.
Descripción de la actividad
Con ayuda de una hoja de cálculo el equipo analizara en una tabla diferentes datos para resolver el problema y graficara en una grafica de dispersión lineal las variables que representan la tabla. Este análisis se subirá en GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, en el área de archivos (incluir una portada con los integrantes de cada equipo).
6. Estudio gráfico con GEOGEBRA.
Tarea
El alumno analizara la grafica del modelo algebraico que representa el problema.
Descripción de la actividad
Con ayuda de GEOGEBRA el equipo graficara la función lineal que representa el problema y realizaran sus observaciones del comportamiento de dicha grafica.
En la grafica señalara la ordenada al origen y determinara la pendiente, realizando observaciones de cómo se determinaría la pendiente con dos puntos contenidos en la grafica de dicha función.
Por lo tanto también presentara un informe con sus procedimientos y resultados en GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, en el área de archivos (incluir una portada con los integrantes de cada equipo). .
Evaluación
Trabajo Final
Cada equipo juntara lo realizado en las actividades 3, 4, 5 y 6 y realizaran un trabajo final que contenga estas actividades.
Descripción de la actividad
El equipo realizara un trabajo final con las actividades realizadas y se subirán a su blog y se enviara al profesor a su correo electrónico.
El trabajo consta de una portada con los integrantes del equipo y su trabajo final.
1. Los alumnos se organizaran en equipos de máximo 5 integrantes, cada equipo seleccionara un nombre y un jefe de equipo con el cual tendrán que crear:
• Una cuenta de correo electrónico en GMAIL
• Una cuenta en la red social FACEBOOK
• Un BLOG en BLOGSPOT.
El correo electrónico creado se enviara al profesor para integrarlo al grupo de trabajo creado en GOOGLE grupos con el nombre de CCH AZCAPÓ VICTOR OLIVA.
En este grupo subirán sus actividades con el nombre del equipo y numero de grupo al que pertenecen.
2. En FACEBOOK se subirá una foto de los integrantes del equipo edita en http://www.picnik.com/ y se mandara la liga o invitación a FACCEBOOK al profesor para ver dicha actividad, dicha foto también se publicara en el blog que ustedes crearon.
3. Investigación de conceptos de:
• Función y relación,
• Función Lineal,
• Grafica de una función lineal,
• Elementos de la grafica de una función lineal.
Foro
Los equipos participaran en el foro para analizar los conceptos anteriores.
Descripción de la actividad
Se investigaran en internet conceptos de función y relación, función lineal, grafica y elementos de una función lineal. Entraran a GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, y participaran en debates (foro) escribiendo las definiciones encontradas, si algún equipo encontró la misma que ustedes podrán a completar o describir algún ejemplo. Cada equipo tendrá como mínimo dos participaciones en el debate y incluirán una bibliografía o página de internet de donde y quien publica dicha definición o investigación.
4. Situación que describe un comportamiento lineal.
Tarea
Cada equipo buscara ejemplos en la vida cotidiana que describa el comportamiento de una variación lineal.
Descripción de la actividad
Los integrantes de cada equipo tendrán que discutir el problema propuesto y realizar un análisis de cómo desarrollarían el ejemplo para poder resolverlo. Podrán proponer las tres formas para representarlo. Trabajo se explicara en una cuartilla y se subirá a GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, en el área de archivos se subirá dicho trabajo (incluir una portada con los integrantes de cada equipo).
5. Propuesta solución hoja cálculo.
Tarea
El equipo resolverá dicho problema realizando una tabla de datos y graficara dichos elementos de la tabla.
Descripción de la actividad
Con ayuda de una hoja de cálculo el equipo analizara en una tabla diferentes datos para resolver el problema y graficara en una grafica de dispersión lineal las variables que representan la tabla. Este análisis se subirá en GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, en el área de archivos (incluir una portada con los integrantes de cada equipo).
6. Estudio gráfico con GEOGEBRA.
Tarea
El alumno analizara la grafica del modelo algebraico que representa el problema.
Descripción de la actividad
Con ayuda de GEOGEBRA el equipo graficara la función lineal que representa el problema y realizaran sus observaciones del comportamiento de dicha grafica.
En la grafica señalara la ordenada al origen y determinara la pendiente, realizando observaciones de cómo se determinaría la pendiente con dos puntos contenidos en la grafica de dicha función.
Por lo tanto también presentara un informe con sus procedimientos y resultados en GOOGLE grupos en el grupo CCH AZCAPÓ VICTOR OLIVA, en el área de archivos (incluir una portada con los integrantes de cada equipo). .
Evaluación
Trabajo Final
Cada equipo juntara lo realizado en las actividades 3, 4, 5 y 6 y realizaran un trabajo final que contenga estas actividades.
Descripción de la actividad
El equipo realizara un trabajo final con las actividades realizadas y se subirán a su blog y se enviara al profesor a su correo electrónico.
El trabajo consta de una portada con los integrantes del equipo y su trabajo final.